Quando se formula uma hipótese em relação a uma determinada característica de uma população, há duas alternativas para a amostra dela retirada:
pertence à população de origem, portanto as diferenças observadas são decorrentes de flutuações normais ou não pertence a essa população e as diferenças encontradas representam um efeito real, não podendo ser atribuídas ao acaso.
O que é "significância estatística" (nível-p)
A significância estatística de um resultado é uma medida estimada do grau em que este resultado é "verdadeiro" ( de que seja realmente o que ocorre na população).
Quanto mais alto o nível-p, menos se pode acreditar que a relação observada é um indicador confiável.
Especificamente, o nível-p representa a probabilidade de erro envolvida em aceitar o resultado observado como válido, isto é, como "representativo da população".
Nível de significância
São os limites que se toma como base para afirmar que um certo desvio é decorrente do acaso ou não. A partir de um nível de significância ( alfa ) convencionado os desvios são devidos à lei do acaso e o resultado é considerado não significativo.
São aceitos como estatisticamente significativos os níveis P = 0,05 e P = 0,01, ou seja, 5% e 1% respectivamente.
Na prática considera-se satisfatório o limite de 5% de probabilidade de erro, não sendo significativas as diferenças que tiverem uma probabilidade acima desse limite. O nível de significância deve ser estabelecido antes do experimento ser realizado e é o risco que se corre de rejeitar uma hipótese verdadeira ou aceitar
Por exemplo, um nível-p de 0,05 indica que há 5% de probabilidade de que a relação entre as variáveis, encontrada na amostra, seja um "acaso feliz".
Assumindo que não haja relação entre aquelas variáveis na população, e o experimento de interesse seja repetido várias vezes, poderia-se esperar que em aproximadamente 20 realizações do experimento haveria apenas uma em que a relação entre as variáveis em questão seria igual ou mais forte do que a que a amostra anterior.
Como determinar que um resultado é "realmente" significante?
A seleção de um nível de significância acima do qual os resultados serão rejeitados como inválidos é arbitrária.
Na prática, a decisão final depende de: se o resultado foi previsto a priori ou apenas a posteriori no curso de muitas análises e comparações efetuadas no conjunto de dados; no total de evidências consistentes do conjunto de dados; e nas "tradições" existentes na área particular de pesquisa.
Em muitas ciências resultados que atingem nível-p 0,05 são considerados estatisticamente significantes, mas este nível ainda envolve uma probabilidade de erro razoável (5%).
Resultados com um nível-p 0,01 são comumente considerados estatisticamente significantes, e com nível-p 0,005 ou nível-p 0,001 são freqüentemente chamados "altamente" significantes.
Significância estatística e o número de análises realizadas
Quanto mais análises realizadas em um conjunto de dados, mais os resultados atingirão "por acaso" o nível de significância convencionado.
Por exemplo:
ao calcular correlações entre dez variáveis (45 diferentes coeficientes de correlação), seria razoável esperar encontrar por acaso que cerca de dois (um em cada 20) coeficientes de correlação são significantes ao nível-p 0,05, mesmo que os valores das variáveis sejam totalmente aleatórios, e aquelas variáveis não se correlacionem na população.
Intervalo de confiança
Uma vez conhecido a média, o desvio padrão e a distribuição das médias amostrais, é possível “melhorar” a nossa estimativa para uma dada média amostral.
Como valor da média varia de amostra para amostra. Podemos melhorar a estimativa da nossa média calculando um intervalo de confiança (IC) para a média que obtivemos. Como?
Recorrendo à variável z, que corresponde a uma distribuição normal padronizada.
Se conhecemos a média amostral e o desvio padrão populacional, podemos pensar em termos probabilísticos para a nossa média.
Basta estabelecermos a probabilidade de acerto para a média e poderemos definir um intervalo esperado para a média que atenda a dada probabilidade.
Este intervalo é chamado de intervalo de confiança.
Então se obtivermos um intervalo de confiança para o parâmetro para cada uma dentre 100 amostras aleatórias da população, somente 5, em média destes intervalos de confiança não conterão.
Exemplo:
Tomamos a massa de uma amostra aleatória de 49 indivíduos e encontramos a média igual a 60 kg e desvio padrão igual a 5 kg. Determine um intervalo para a média com 90%, 95% e 99% de certeza.
Temos uma média amostral x . Sabemos que, para o n dado (49), podemos dizer que a distribuição das médias amostrais é normal.
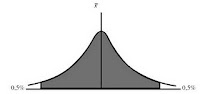
90% de certeza, significa dizer que queremos estimar a média populacional com 90% de probabilidade de acerto, logo, a área pintada.
Agora podemos lançar mão da tabela da estatística z para encontrar o valor z correspondente.
Observe que, como a distribuição é simétrica em relação à média, queremos os 45% acima e os 45% abaixo da média. Lançando mão da tabela, verificamos que o valor de z para P = 0,45 (45%) é 1,65.
Graus de liberdade
É o número de classes de resultados menos o número de informações da amostra que é necessário para o calculo dos valores esperados em cada classe.
GL = n - 1, em que n = número de classes
No caso de lançamento de um dado seriam 5 os graus de liberdade.
Probabilidade de X assumir um valor em um dado intervalo
-como lidamos com variáveis contínuas na distribuição normal, não se pode determinar a probabilidade da variável ser exatamente igual a um dado valor, uma vez que a área da curva correspondente a qualquer ponto ao longo da curva é infinitesimal; entretanto, pode-se calcular a probabilidade da variável assumir um valor entre dois pontos
-neste caso, usamos uma tabela da distribuição normal padronizada, ou seja, que possui µ=0 e s=1
-para transformar uma variável de forma que tenha média 0 e desvio padrão 1 (padronização ou normalização), basta fazer o cálculo:
Desvio Padrão de Médias Amostrais (erro padrão da média)
-quão acurada é uma média amostral em relação à média populacional (µ)?
-diversas amostras tomadas de uma mesma população produzem estimativas de médias diferentes entre si e diferentes da média populacional
-dado um número grande de amostras, as médias dos valores das estimativas amostrais tendem a coincidir com as estimativas populacionais
As rendas mensais dos graduados em um curso de especialização em uma grande empresa são normalmente distribuídas com uma média de R$ 2000 e um desvio padrão de R$ 200. Qual é o valor de Z para uma renda X de R$ 2200? R$ 1700?
· Para X = 1700
Um valor de Z = 1 indica que o valor de R$ 2200 está localizado 1 desvio padrão acima da média de R$ 2000.
Um valor de Z = -1,5 indica que o valor de R$ 1700 está localizado 1,5 desvio padrão abaixo da média de R$ 2000.
A informação que temos agora é que, 60 é a média da amostra, mas se fosse tomada uma outra amostra de 49 indivíduos, a média poderia assumir qualquer valor dentro de um dado intervalo, e que o intervalo pode ser maior ou menor de acordo com o grau de certeza ou probabilidade que se queira.
Mostra que se olhamos para duas médias pura e simplesmente, mesmo que elas sejam diferentes, podem não ser estatisticamente diferentes.
Testes de Hipóteses
Hipótese: é uma conjectura, uma resposta provisória que, de acordo com certos critérios, será rejeitada ou não rejeitada
Estimação:
Procedimento estatístico que permite prever, com certa probabilidade o valor de um parâmetro desconhecido(populacional) a partir de informações colhidas em amostras.
A hipótese que será testada chama-se em estatística de Hipótese Nula (H0).
Nesta decisão pode-se cometer erros, ou seja é possivel rejeitar uma hipótese mesmo ela sendo verdadeira. Esta probabilidade chama-se de nível de significancia.
Então estabelece uma região crítica e uma região não crítica. Se o valor pertencer a região crítica a hipótese deverá ser rejeitada.
Se o teste for de diferença o teste é Bicaudal
Se o teste for > ou < o teste é Unicaudal
Unicaudal direita
< Unicaudal esquerda
Distribuição Normal
Um construtor supõe que a qualidade dos tijolos que utiliza em suas obras está apresentando variações. Em face da experiência anterior sabe-se que a resistência média ao rompimento de tais tijolos é de 200 Kg com um desvio padrão de 20Kg. Numa amostra de 100 tijolos apurou-se que a resistência ao rompimento alcançou um total de 19.600Kg. Fixado o nível de significância de 0,05, verifique se a qualidade dos tijolos está apresentando variações ( teste bilateral).
Ho : m = 200
H1 : m 200
Z de rejeição
Nível de significância = a = 5%
n = 100
S x = 19.600
s = 20 ® é da população
Z = 1,96 (tabela z)
pop. infinita ® não se sabe a quantidade de tijolos.
0,025 0,025
Z=-1,96 Z=1,96
-2 está na Z de rej.
Rejeita-se Ho ao nível de significância de 5%.
Logo os tijolos estão apresentando variações.
Estimativa do erro padrão com apenas uma amostra
Nesse caso, os parâmetros da população (desvio padrão e média) são conhecidos.
z = (x - m) / sx
Exemplo: Um médico receitou um medicamento vasodilatador (Nifedipina) para Hipertensão Arterial, mas ele suspeita que o medicamento está aumentando a freqüência cardíaca dos pacientes. Sabedor que a população apresenta os seguintes valores: m = 69,8 , s = 1,86, coletou uma amostra aleatória de 50 pacientes e mediu as suas freqüências cardíacas, obtendo a média de 70,5. Ele estava correto?
Estabelece-se as hipóteses, com a = 5%
Hipótese Nula = x - m = 0 ou seja, H0 = x < m
H. Alternativa = x - m ¹ 0 ou seja, Ha = x > m
Calcula-se o erro da média:
sx = s / Ö n = 1,86 / Ö 50 = 1,86 / 7,0710 = 0,2630
Calcula-se z
z = (x - m) / sx = (69,8 - 70,5) / 0,2630 = -0,7 / 0,2630 = -2,66
Consultando o valor -2,66 na tabela de z obtém-se o valor 0,4961. Portanto:
z = 0,50 - 0,4961 = -0,0039 = 0,39%
Ou seja, existe uma chance de aproximadamente 0,39% de que seja obtida uma média maior do que 70,5 ao acaso, quando são retiradas amostras aleatórias de tamanho 50 desta população. Como essa probabilidade é menor que 5% (p < 0,05), rejeita-se H0 e aceita-se H1, concluindo-se que a nifedipina aumentou significativamente a freqüência cardíaca.
Exemplo: Dois tipos de pneus são fabricados. O tipo A tem variabilidade de duração = 2.500 Km, e o tipo B tem = 3.000. Uma amostra testou 50 pneus do tipo A e 40 do tipo B, obtendo 24.000 km e 26.000 Km de duração média dos respectivos tipos. Adotando-se um risco alfa de 4%, testar a hipótese de que a duração média é a mesma.
1. Ho: 1 - µ2 = 0 1 = µ2
H1: 1 µ2 ou 1 - µ2 0
2. Fixar .= 0,04 Escolher a variável normal padrão Z.
3. Com auxílio da tabela Z, determinar as áreas de aceitação e de rejeição de Ho.
RC (0,02) RA ( 0,96) RC( 0,02)
-2,05 0 2,05
4. Cálculo do valor da variável.
= -3,38
5. Conclusões:
Como Zcal -2,05 , rejeita-se Ho, concluindo-se com o risco de 4% que a duração média dos pneus são diferentes.
Teste t
A distribuição t de student
A rigor, a utilização da distribuição z para a determinação de um intervalo de confiança para a média amostral, só seria possível se o desvio padrão populacional fosse conhecido (diferentemente da forma que calculamos acima). Entretanto, isso não ocorre na maioria dos estudos, onde se obtém o desvio padrão a partir da amostra estudada.
Uma outra situação que ocorre com freqüência, é o estudo de amostras pequenas (n £ 30). Para resolver os dois problemas acima, existe uma distribuição muito parecida com a distribuição normal, que é a distribuição t de student.
a distribuição de t tem formas diferentes para diferentes graus de liberdade (v, onde v= n-1);
quanto maior o valor de n, mais a distribuição de t se parece com a distribuição normal e, quando n tende ao infinito, as duas distribuições são idênticas
distribuição norma padronizada (linha cheia) e a distribuição t (tracejado
A utilização da distribuição t pressupõe normalidade dos dados da amostra.
Na prática, para amostras pequenas (n £ 30), a população da qual a variável foi submetida à amostragem deve ter distribuição normal para se utilizar a estatística t. Já para amostras grandes, isto não é necessário
A tabela verificamos que existem os valores de t para as probabilidades 0,10; 0,05; 0,025; 0,01; e 0,005; considerando uma cauda, ou seja, probabilidade de um valor maior ou de um valor menor que t.
Portanto, se queremos intervalos de confiança para a média amostral, devemos calcular: 1 - o valor do intervalo de confiança desejado, multiplicar este valor por 2 e buscar o valor de t na tabela correspondente à área nas duas caudas.
A fórmula que define o intervalo de confiança para a média é:
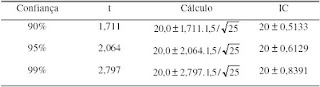
Exemplo 1: Considere que de uma amostra de 25 indivíduos, obteve-se média 20,0 e desvio padrão 1,5. Determinar intervalo de confiança para a média, considerando a confiança de 90%, 95% e 99%.
Solução: Primeiro temos que encontrar o valor de t. Temos o gl que é 24 (25 – 1).
Precisamos encontrar t para as áreas bicaudais de 10%, 5% e 1%. A tabela abaixo
Mostra os valores de t e os cálculos respectivos.
O teste de Qui Quadrado
Testa basicamente dois tipos de hipóteses: Aderência e Independência
É um teste de hipóteses que se destina a comparar proporções.
Teste de Aderência serve para ajudar o pesquisador a decidir se os dados que ele colheu se ajustam bem a uma determinada lei.
Ou seja, é usado para:
- Verificar se a freqüência com que um determinado acontecimento observado em uma amostra se desvia significativamente ou não da freqüência com que ele é esperado. - Comparar a distribuição de diversos acontecimentos em diferentes amostras, a fim de avaliar se as proporções observadas destes eventos mostram ou não diferenças significativas ou se as amostras diferem significativamente quanto às proporções desses acontecimentos.
Qui-quadrado
distribuição de qui-quadrado: variável assume qualquer valor real (contínua) e a frequência (f1) de uma observação de valor X1 é definida por:
Karl Pearson propôs a seguinte fórmula para medir as possíveis discrepâncias:
c2 = ∑ [(o -e)2 /e]
em que
o = freqüência observada para a classe,
e = freqüência esperada para aquela classe.
Por exemplo: Se uma moeda não viciada for jogada 100 vezes, espera-se obter 50 caras e 50 coroas, já que a probabilidade de cair cara (p) é = a ½ e a de cair coroa (q) também é = a ½. Entretanto, na prática, é muito difícil obter valores observados, idênticos aos esperados, sendo comum encontrar valores que se desviam dos teóricos.
Supondo que obtenha-se 60 caras e 40 coroas. Qual será o valor de c2 ?
c2 = [(60 – 50)2 / 50] + [(40 – 50)2 /50]
portanto, c2 = 2 + 2 = 4
Graus de liberdade
Número de linhas de dados – 1
Glib = (l –1 )
Ou
Glib = (c-1) x (l-1)
Teste de independência
Serve para decidir se duas variáveis estão ou não amarradas uma à outra por uma relação de dependência
Quanto menor a dependência entre duas variáveis menor o valor de qui calculado.
Correção de Yates (Correção de continuidade)
Quando se obtém um valor de c2 significativo mas nota-se que a freqüência esperada em uma das classes é pequena (tipicamente, quando for menor que 5) a fórmula de obtenção de c2 poderá produzir um valor maior que o real.
Então, Fisher recomenda que seja utilizada a correção de Yates:
c2 = S [(
o -e
- 0,5)2 /e
Evidentemente não é preciso usar a Correção de Yates se o valor de c2 obtido for menor que c2c , pois o novo valor será menor que o primeiro, continuando a não ser significativo. Portanto, de modo geral, usa-se a correção de Yates quando - há pelo menos uma classe com número de esperados menor que 5 e - o valor de Qui Quadrado obtido é maior que o crítico
UM GRAU DE LIBERDADE
Quando há apenas duas categorias, há um grau de liberdade e a correção de Yates é usada. Podemos testar a hipótese nula que a razão entre macho : fêmea não é diferente de 1 : 1. Uma amostra de 16 larvas coletadas e criadas até adulto contém 12 machos e 4 fêmeas (Fowler & Cohen, 1990). Esta razão é significativamente diferente de 1 : 1?
O valor de qui-quadrado 3,0625 é menor que o valor crítico com v=1, portanto aceitamos a hipótese nula.
Importante: os indivíduos de cada sexo devem ser dispersos em uma maneira independente.
Como usar a tabela de Qui Quadrado
Na coluna referente a 5% de probabilidade encontra-se o valor crítico de qui quadrado (c22), com o qual deve ser comparado o valor calculado de c22.
Aceita-se a hipótese de igualdade estatística entre os números de observados e de esperados.
Os desvios não são significativos.
Rejeita-se a hipótese. Os números de obs e esp são estatisticamente diferentes. Os desvios são significativos..
Qui quadrado e o Teste de Heterogeneidade entre amostras
Por vezes, na análise de dados experimentais é preciso comparar as variâncias de duas amostras aleatórias independentes, para nos certificarmos se as amostras foram retiradas de distribuições com variâncias iguais.
Na próxima postagem vamos falar sobre incerteza de medição.
Obrigado.











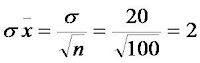













0 comentários:
Postar um comentário